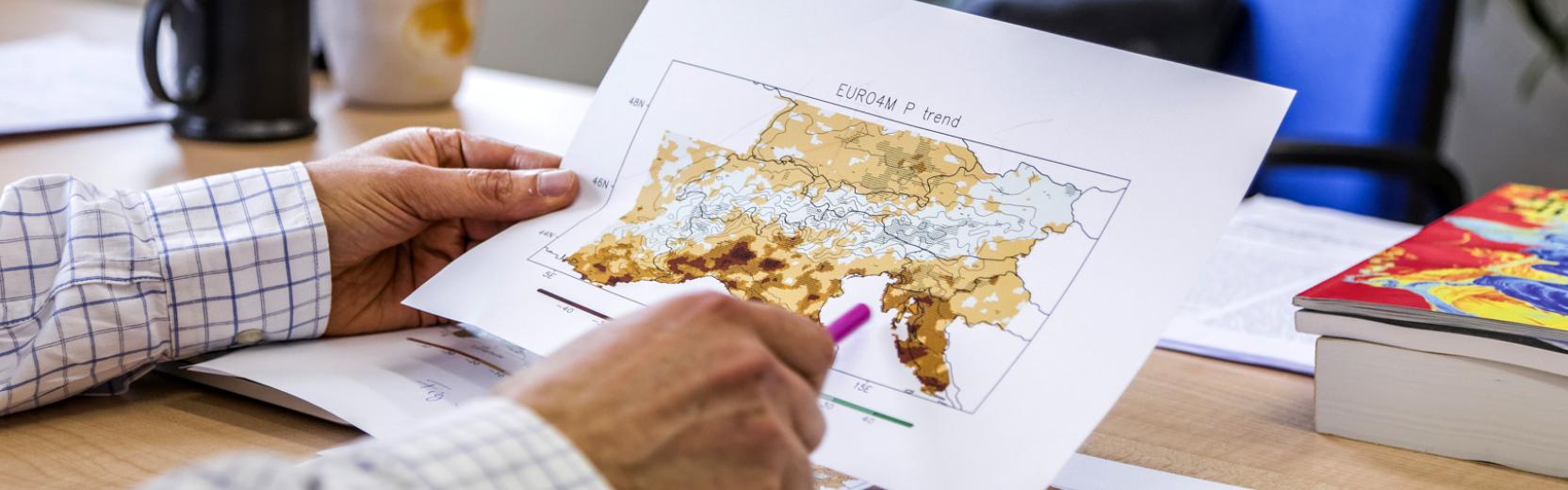
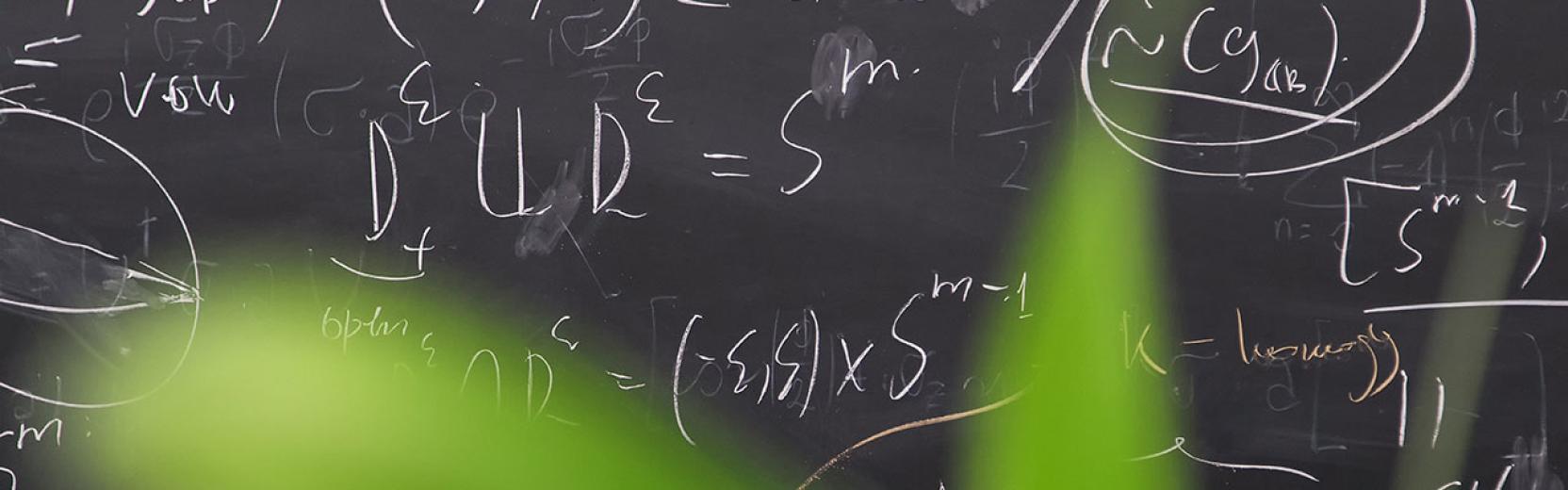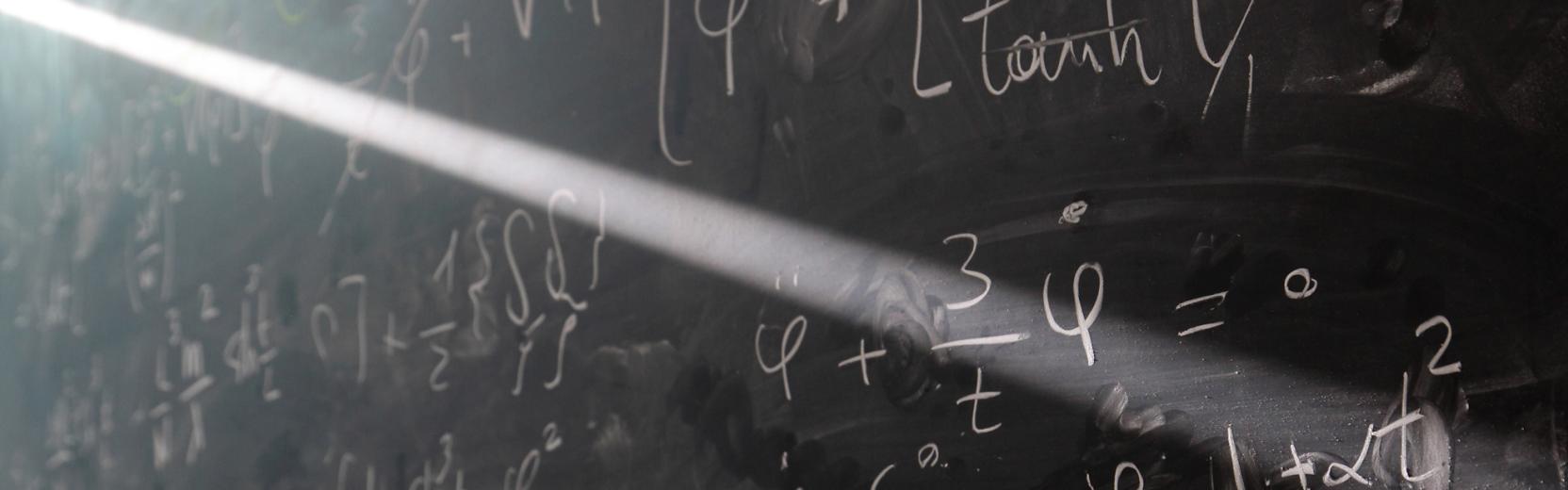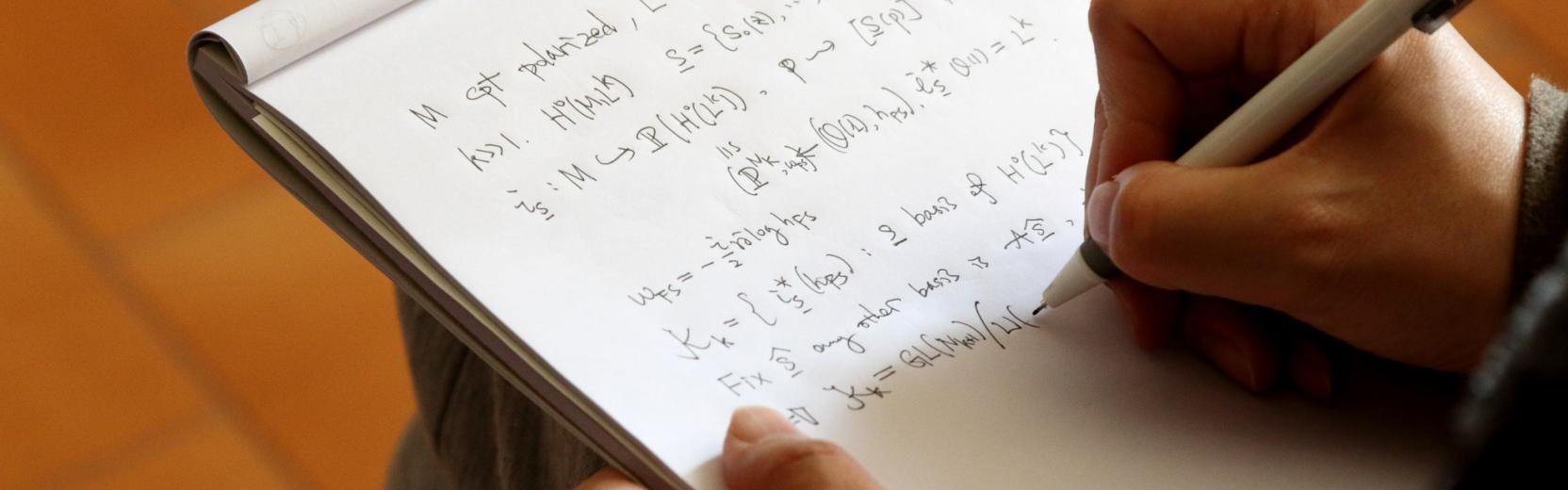Harmonic analysis provides the mathematical foundation for the study of many sorts of oscillatory phenomena in nature. In mathematical language, such phenomena are usually modelled through the…
Research Areas
view allDifferential Geometry is the mathematical theory of curvature of spaces of arbitrary dimension. Two of its major classical themes are to determine the "best" metric on a given space (for example…
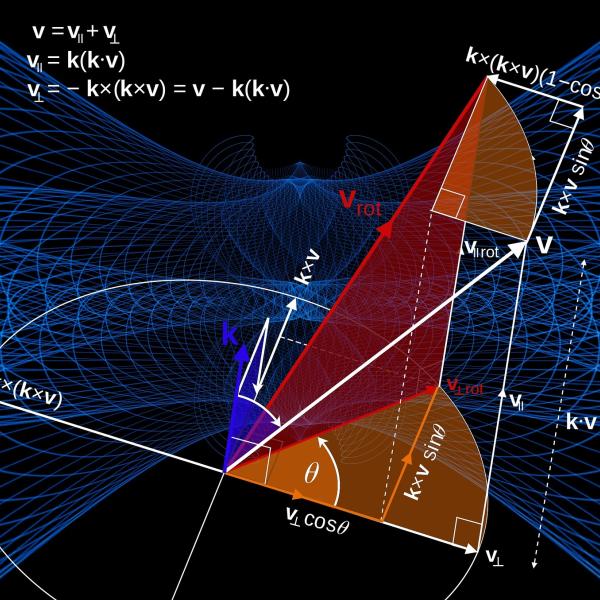
Most (if not all) physical processes are “deterministic”, in the sense that they are governed by physical laws which completely determine their evolution in time. The development of the Theory of…

Algebraic Geometry classically studies the solutions of polynomial equations in several variables, the so-called algebraic varieties. Today also various generalisations of these are used and…
Theoretical physics, and in particular the area of Quantum Field Theory and String Theory, has been known to be a rich source of non-trivial mathematical conjectures and constructions. An example…

The performance of modern inference and learning algorithms exploiting massive datasets for data science applications is improving at an incredible pace. Yet, the development of a theoretical…

Permanent Scientists
view all membersClaudio Arezzo

Jean Barbier

Emanuel Carneiro

Lothar Göttsche

Stefano Luzzatto

Alina Marian

Pavel Putrov