Researchers in ICTP's Mathematics section investigate a wide range of topics, including:
Back
Researchers in ICTP's Mathematics section investigate a wide range of topics, including:

Harmonic analysis provides the mathematical foundation for the study of many sorts of oscillatory phenomena in nature. In mathematical language, such phenomena are usually modelled through the Fourier transform and other types of oscillatory integrals; these are important tools in the theoretical background of telecommunications, biomedical equipment and data compactification processes. Analytic number theory is one of the most classical subjects in mathematics, aiming to study structures related to the integer numbers and their building blocks, the prime numbers, using tools from analysis; one of the most celebrated open problems in the field is the Riemann hypothesis (RH) of 1859, predicting the alignment of the complex zeros of the classical Riemann zeta-function. ICTP mathematicians investigate several themes at the interface between these two fields, including: sharp inequalities in Fourier restriction theory, oscillatory behaviour of maximal functions, approximation theory, and Fourier optimisation tools in the study of objects related to the Riemann zeta-function and other L-functions.
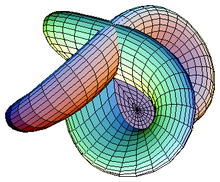
Differential Geometry is the mathematical theory of curvature of spaces of arbitrary dimension. Two of its major classical themes are to determine the "best" metric on a given space (for example which spaces admit a metric of constant positive Ricci or Scalar curvature) or to determine the "best" submanifold among a determined class of competitors (for examples finding a closed geodesic or a volume minimiser in its homology class). Combining techniques from the Calculus of Variations, PDEs and Algebraic Geometry, the Differential Geometry group at ICTP studies various aspects of the above questions especially in Complex Geometry, and their connection with many physical problems arising in General Relativity, Cosmology and Condensed Matter Physics.

Most (if not all) physical processes are “deterministic”, in the sense that they are governed by physical laws which completely determine their evolution in time. The development of the Theory of Differential Equations initiated by Newton and Leibniz in the 17th century gave scientists the hope that knowledge of these physical laws could help to predict the evolution of a system. However, many systems -- ranging from complicated ones such as the weather to very simple systems such as flipping a coin -- seem to defy these expectations and remain very unpredictable, notwithstanding our knowledge of the underlying physical laws. Over the last hundred years there has been an increasing understanding of how deterministic systems can be unpredictable and “chaotic". The main mathematical tools used to understand and explain this phenomenon are those of (Smooth) Ergodic Theory, which combines ideas from various areas of mathematics (such as Analysis, Topology, Geometry, Probability Theory, and others) in an interdisciplinary approach to understand and describe the Statistical Properties of Deterministic Dynamical Systems.
Algebraic Geometry classically studies the solutions of polynomial equations in several variables, the so-called algebraic varieties. Today also various generalisations of these are used and studied, for instance schemes, algebraic stacks, and derived schemes. Modern Algebraic Geometry is a central area of mathematics, with close ties to many other fields of mathematics from which it uses their methods and results. Among these are Algebra, Complex Analysis, Differential Geometry, Topology, Number theory and mathematical physics. At ICTP a special emphasis is on the study of moduli spaces, which are algebraic varieties parametrising interesting objects in algebraic geometry, like curves, vector bundles or sheaves on varieties. This includes the study of their topological invariants, applications in enumerative geometry (counting objects with prescribed properties) and exploring the relations.

Theoretical physics, and in particular the area of Quantum Field Theory and String Theory, has been known to be a rich source of non-trivial mathematical conjectures and constructions. An example of such a construction is Topological Quantum Field Theory, a notion that was first formalised by Michael Atiyah in the 1980s and underwent various generalisations later. It incorporates topological invariants of manifolds and embeddings into an algebraic structure which is convenient to study. This and other mathematical notions closely related to theoretical physics are some of the research subjects at ICTP.

The performance of modern inference and learning algorithms exploiting massive datasets for data science applications is improving at an incredible pace. Yet, the development of a theoretical framework to model these complex information processing systems and better quantify their potential and limits is still at its premises. ICTP mathematicians, together with their colleagues in ICTP's QLS section, investigate fundamental questions such as "What is the minimal amount of data needed to perform accurate predictions? When is it possible to infer and learn in a computationally efficient manner? What is the influence of data structure on the performance of inference algorithms?" The answers happen to be deeply linked to phase transition phenomena as arising in more classical physical systems. But this is more than an analogy. Therefore, to tackle these timely problems in a quantitative, mathematically rigorous manner, we often take an approach rooted in statistical physics combined with information theory, high-dimensional statistics, random matrix theory and the mathematical physics of spin glasses.