ICTP Welcomes New Ramanujan International Chair

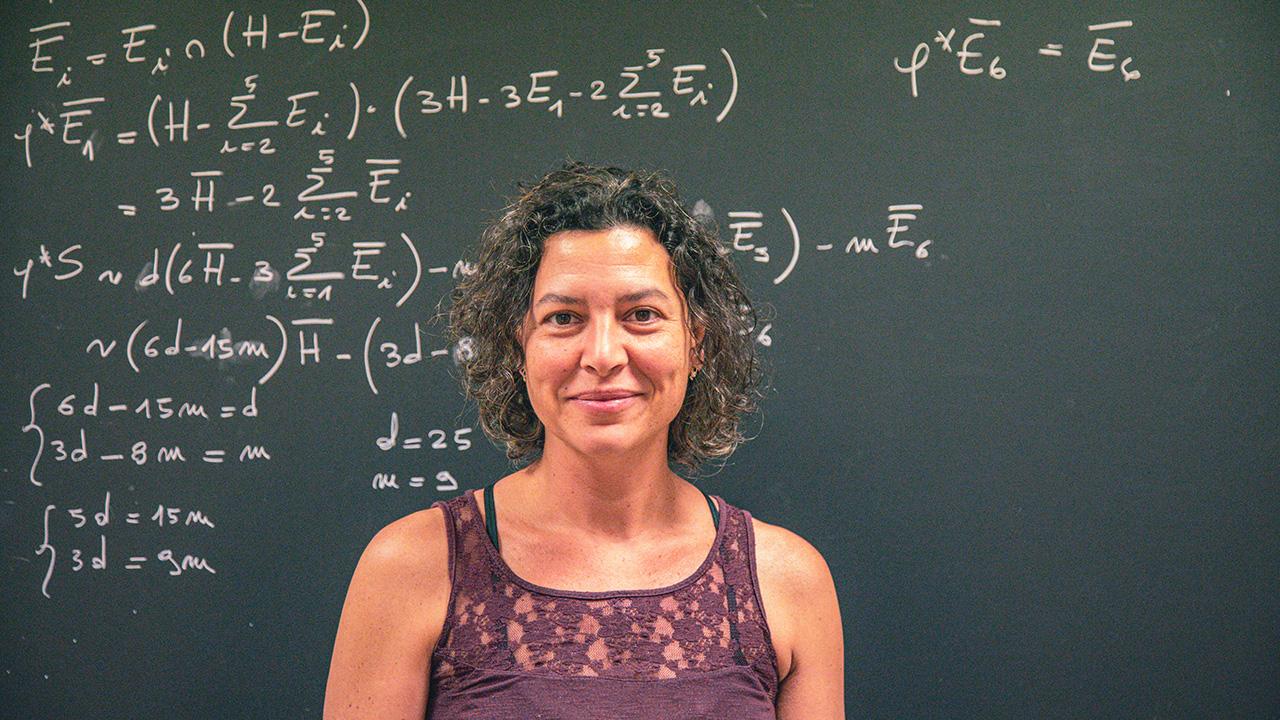
Carolina Araujo, a professor at the Institute for Pure and Applied Mathematics (IMPA) in Rio de Janeiro, Brazil, is the new holder of the Ramanujan International Chair.

An algebraic geometer specializing in birational geometry and foliations, Araujo is a distinguished mathematician and a promoter of women in mathematics. She won the L'Oreal Award for Women in Science in Brazil in 2008 and was an organizer and an invited speaker at the International Congress of Mathematicians in 2018, where she also led the inaugural World Meeting for Women in Mathematics ((WM)2). She currently chairs the Committee for Women in Mathematics at the International Mathematical Union.

Araujo’s connections with ICTP are longstanding. She was a Simons Associate between 2015 and 2019, and she was awarded the 2020 DST-ICTP-IMU Ramanujan Prize for Young Mathematicians from Developing Countries. In this interview she discusses her path in mathematics, her passion for algebraic geometry and her commitment to a greater representation of women in mathematics. 

How did you become interested in mathematics?

I have always liked mathematics very much since I was a child. I used to play teacher with my sister and show her the mathematics I knew on the blackboard. Later, in high school, I had the chance to be taught mathematics by someone who encouraged us to think in a more abstract way, beyond the exercises that we were assigned. This was very stimulating, but I did not really know what a career in mathematics was until I arrived at university. At the beginning I thought I was going to be an engineer like my parents, but during the first two years of university I tried different things, attending classes not only in engineering, but also in mathematics, physics and chemistry. When I took the first serious course in mathematics I immediately knew it was my path and I haven't left it since. With time I also found out that it was possible to have a career in research, so I started attending an initiation to research program. It became natural for me to do a PhD after that.

You are an algebraic geometer. Can you tell us in simple words what algebraic geometry is about?

I think of different areas of mathematics similarly to how I think of our senses. We use all our senses, our sight and smell and taste and touch, in order to understand the world that we live in. Similarly, there are many different “mathematical senses” that we can use to better understand a problem in mathematics. Among these many senses there is geometry and there is algebra. Geometry studies the shape of objects. It deals with shapes, angles, the notion of distance. Algebra is a different way of understanding mathematics. It for example tells us how we can manipulate the symbols in an equation in order to find the solution.

Algebraic geometry combines these two senses to help us better understand the mathematical objects that we are interested in so that, for instance, when you look at an equation, you can either consider it as a set of symbols, or as a set of points that satisfy the equation and that have certain geometric properties.

For example, one might want to solve an equation or a system of equations, and not be able to do that explicitly with algebraic methods. One way out is to study the geometric properties of its space of solutions. At other times, we can try to understand the geometric properties of a certain object in space such as, for example, the curvature of a trajectory by analyzing the equation and the algebraic structure behind it.

What are the particular problems that you are interested in?

Some of the projects that I am currently involved in are precisely related to the notion of curvature, which is probably one of the most fundamental concepts in geometry. Roughly speaking, the curvature of a one-dimensional curve measures how it deviates from a straight line. You can also define the curvature of a surface, which measures how it deviates from a flat plane, and so on for higher dimensions.

I am interested in understanding objects that have a constant curvature, from the algebraic point of view. In simple terms, I want to be able to tell whether an object has a constant curvature by looking at the algebraic equations that define it.

What is the mathematical question that you would dream to answer, were you given a magical stick?

There are a few, and some are related to curvature. For example, I believe that a certain class of symmetric spaces that I find very nice and interesting have a constant curvature, but I don't know how to show that yet.

I am also studying a class of spaces that appear across different problems, in different areas of mathematics. I am interested in understanding their curvature properties, but they are also very important from the point of view of what people call moduli spaces in algebraic geometry, and I guess that there is something specific about these spaces that would help us connect the theory of curvature and the theory of moduli spaces. I still don't know what that is, but I would like to find out.

How do you decide which problems to focus on in your research?

The problems that I like to work on are those for which I will have to find a new path – that’s what I find stimulating and fun, and I like problems that make me happy while I work on them.

And where do you get your ideas from?

I think ideas come from everywhere and it’s hard to explain how mathematical inspiration works. What happens to me when I'm working on a problem that I find challenging and that I cannot solve despite working very hard on it, is that the solution comes when I take a break. Something must happen in the brain in that moment of relaxation, which suddenly makes me see some new connection or a clear answer. For me, doing mathematics requires a combination of both a lot of dedication and of moments of quiet, when somehow ideas get together in my mind.

You have been very involved in organizations that promote women in mathematics. What has your experience as a woman in mathematics been? And what motivates your commitment to supporting women in mathematics?

I have not always been so active in supporting women in mathematics, it took longer for me to perceive the gender gap in the field and I imagine this is because I was privileged enough not to experience many of the barriers that usually women mathematicians tend to face. My mother is an engineer and she has always been a model for me, which made it very clear from the beginning that doing math was possible. This is not the case for many women, who sometimes experience prejudice and lack role models. I also feel privileged because my family’s economic situation meant that I had access to good schools and I did not have to face many of the barriers that women or other minorities have to go through.

It is only after talking to many other women and learning about their experiences that I saw the injustices that were around me. They made me upset and at some point I realized that I had the power to do something to change the situation for all women. I naturally embraced this and it has become stronger than me.

You have been a very successful mathematician, whose work has been recognized by the international mathematical community through various important awards. In addition to talent and hard work, what would you single out as the most important factor that helped you make it through?

I think that there are many qualities that are important for a mathematician or for a scientist in general. For example, I am very disciplined and I work a lot, but I am also very patient, which I think is a very precious quality for scientists, as sometimes it just takes long to get answers. Many times I have also been just lucky enough to be in the right place at the right time. I also tend not to let go of opportunities and this has helped me on several occasions.

What are the biggest challenges that you encountered along your path?

The obstacles I encountered are the barriers and challenges typical of a career in science. I remember for example that my first year of PhD was very difficult. I had left my home country to study abroad and was immersed in a different culture, also academically. People there were much more competitive than I was used to. The department I was coming from was very friendly and everyone used to help each other, while I suddenly found myself in a competitive and individualistic environment. It was a cultural shock and I think that was probably one of the most difficult moments in my career. Luckily I received a lot of support from friends and family and in hindsight, after I successfully went through it, I recognise that it made me stronger. Now I look back and I think that yes, it was hard, but I could do it.

You have known ICTP for a long time and between 2015 and 2019 you were a Simons Associate. What has this experience meant to you?

I love ICTP. It is a wonderful place and I feel very inspired here. I visited ICTP many times over the years and I made some important breakthroughs while I was here. For example, the last time that I visited ICTP as part of my associateship, I started working on a new project about K stability, a topic at the frontier between algebraic geometry and differential geometry, which is now very important in my research. When I was here in 2019, we organised a little working group on this subject. I did not know much about it then and it is thanks to this working group that I started learning more, not only from the algebraic point of view, but also from the differential point of view. Over time, I became more and more interested in the topic and together with other collaborators, we wrote a book about it that has now been published. The months that I spent at ICTP were very important for me to set the ground that helped me take on this project. ICTP is and has always been a very inspiring place for me.

As the new holder of the ICTP Ramanujan International Chair you will contribute your knowledge and experience to ICTP. What are the research lines that you would like to pursue and the activities that you most look forward to organizing in collaboration with ICTP researchers?

I hope that we can organize schools or research programs focused on algebraic geometry. I also hope that we will be able to find connections between my topics of expertise and the ones developed by the algebraic geometry group here at ICTP. I work on what we call birational geometry, while here there are very strong researchers working on moduli spaces. Being able to spend more time at ICTP will be a great opportunity to deepen the connections between these two different areas of algebraic geometry and find new ones.

Araujo will visit ICTP in her new role of ICTP’s Ramanujan International chairholder at the end of September 2025.

Here is an extract of the interview: