A Model of Leptons

Fifty years ago today, a manuscript titled “A Model of Leptons” arrived at the offices of Physical Review Letters. It was written by Steven Weinberg, then a 34-year-old visiting professor at the Massachusetts Institute of Technology, on leave from the University of California, Berkeley. Only two and half pages long, the paper brought together an assortment of ideas and neatly constructed a unified theory of the electromagnetic and weak interactions. It spelled out a set of particles that could be searched for (the W, Z, and Higgs), and pointed out that the Z particle would generate a phenomenon called weak neutral currents.

The paper was duly published about a month later, but for the next few years it languished, seemingly barely noticed, cited only a couple of times in other journal papers. Then around 1971 everything changed, as further theoretical studies confirmed a major conjecture of the paper, and theorists warmed to the general approach that it had laid out. Soon thereafter, weak neutral currents were observed, the first of a long line of experimental discoveries confirming predictions of the model. By 1976, “A Model of Leptons” was the most cited high-energy physics paper on record, a position it held for more than 30 years—an astonishing run that cannot be eclipsed earlier than the year 2044. The 1979 Nobel Prize in physics was awarded to Weinberg, along with Abdus Salam (who had independently developed the same model by 1968) and Sheldon L. Glashow (who published an important precursor in 1961). Salam, of course, was also the founder of the ICTP.

Today, Weinberg and Salam’s model of leptons is one of the central parts of the Standard Model of particle physics. The experimental confirmations have continued, including discovery of the W and Z particles in 1983, highly detailed verification that their properties match the predictions of electroweak theory, and discovery of the Higgs particle at the Large Hadron Collider (LHC) in 2012. So far, the Higgs seen at the LHC looks just like the Higgs of Weinberg’s model. Fernando Quevedo, director of the ICTP (and a graduate student of Weinberg’s in the 1980s), suggests that the 1967 paper may be the most important paper of the last 60 years or so. “It is one of those things that will remain in history,” he said, “because it combined electromagnetism with the weak interaction. And it is not only the unification, it is understanding the nature of the weak interaction.”

Quevedo fondly remembers the excitement of two occasions when predictions of Weinberg’s model were confirmed. The first was in 1983 when he was graduate student at the University of Texas at Austin. “In one of Weinberg’s lectures he came in and told us, ‘well, my contacts at CERN just told me that they discovered the W particle!’ He was excited and we were all excited. I remembered that feeling some 30 years later, when I was present when they announced the Higgs discovery.”

A Quest for a Theory

The Standard Model is one of the crowning achievements of twentieth century science. Along with general relativity, it provides the basis for understanding essentially everything in the nearby world around us: It specifies the properties of the particles that make up all material objects, including ourselves, and also more ethereal entities such as radio waves, beams of light, and an invisible flood of neutrinos passing through us from the sun. It accounts for all the particles observed so far in our most ingenious and expensive experiments, like the LHC.

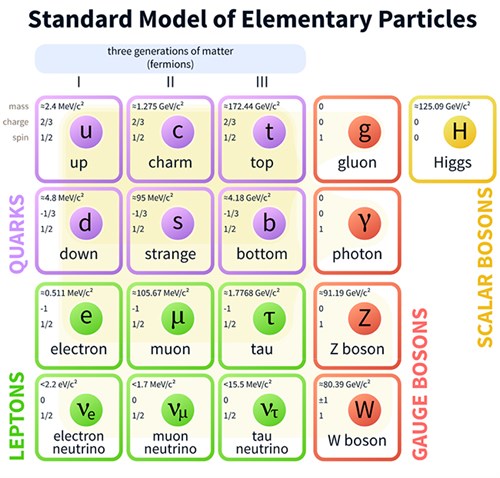The Standard Model also describes the forces (except for gravity) by which all those particles influence one another. These include electromagnetism, which drives so much of our technology and is also involved in the properties of atoms and chemical reactions. Then there is the strong force, which rules supreme in the nuclei of atoms, forming the tight little blobs (“protons” and “neutrons”) that embody most of the mass we routinely encounter. Finally, there is the weak force, which triggers certain types of radioactive decays as well as reactions that are vital in the chain of processes powering the sun and stars.

In our everyday world, only gravity (which is well-described by Einstein’s general theory of relativity) lies outside the purview of the Standard Model. To be sure, we still need chemistry and materials science and fluid dynamics and biochemistry and biology and neuroscience and on and on, to understand or describe “everything,” but in principle those worthy disciplines all trace back ultimately to the bedrock that is the Standard Model.

Fifty years ago, the Standard Model did not yet exist. Physicists were still grasping for an adequate mathematical theory to describe the strong and weak interactions. At the level of particle physics, electromagnetism was extremely well described by a quantum field theory. In that paradigm, electromagnetic interactions arise from the exchange of photons, the quantum particles of light. The quantum field theory of photons (quantum electrodynamics, or QED) is a so-called gauge theory. The photons are massless, they are “vector” particles (this is related to polarization of light), and a mathematical symmetry called gauge invariance essentially dictates how they interact with charged particles. By 1961, QED was the epitome of a good theory, and physicists were striving to come up with a corresponding theory for the strong and weak interactions.

The weak interaction in particular had some tantalizing similarities to electromagnetism. Both seemed to involve vector particles (or “vector bosons”), and both were relatively universal (they interact with essentially everything). The strong force, by contrast, only affected a class of particles dubbed hadrons, leaving the other class of particles (leptons) immune. (Leptons include electrons and neutrinos. Hadrons include the proton and neutron.) Despite the similarities between electromagnetism and the weak interaction, their differences presented major obstacles to unification.

The Elements Come Together

 The gauge symmetry underlying the weak theory had to be more complicated than that of the photon, and that could be accommodated by a type of gauge theory developed by C. N. Yang and Robert Mills in the 1950s. Sheldon Glashow’s contribution in 1961 was to construct a theory with the correct gauge symmetries to include both electromagnetic and weak interactions. The theory started with four vector bosons. Two of these were charged, and would mediate the known weak interactions involving electrons and neutrinos. The other two bosons were neutral (like a photon). These two mixed together, with one part becoming the familiar massless photon, the other part becoming a neutral component of the weak interaction.

 To match observations, however, the weak vector bosons needed to be very heavy (if they were massless, they would surely generate a long-range force like electromagnetism, but weak interactions were known to be very short range). On the other hand, Yang-Mills theories required massless particles. Other desired properties of electroweak theory were spoiled by the small but nonzero mass of the electron. Glashow’s theory did not adequately solve this part of the problem.

In 1964, Peter Higgs, Robert Brout, François Englert, Gerald Guralnik, C. R. Hagen, and Tom Kibble developed a theory now known as the Higgs mechanism. This provided a way to have a Yang-Mills gauge theory in which the gauge bosons manifest as massive particles. The theory begins with massless gauge bosons as usual, but also contains a group of very featureless particles known as scalar particles. The underlying equations of the theory have the full gauge symmetry. Interactions between the scalar particles are set up in special way. In QED, the lowest-energy state of the theory is when the electromagnetic field vanishes. After all, this corresponds to what we are accustomed to: zero field, zero energy. In contrast to this, the scalar particles in the Higgs theory have their lowest energy when one of them acquires a specific nonzero value. In a universe described by these equations, in its natural vacuum state of lowest energy it will be permeated by a nonzero scalar field. In this state with a nonzero field, the gauge symmetry is broken, and the gauge bosons behave like massive bosons. This is known as spontaneous symmetry breaking. The breaking is “spontaneous” because it arises spontaneously when the universe settles down into the low-energy state with that nonzero background field.

Finally we come to Weinberg and Salam’s contribution: Their model uses the Higgs mechanism to provide a mass to the weak gauge bosons with the gauge symmetry outlined by Glashow. This approach leads to a more tightly constrained theory, which allows more properties of the resulting W and Z bosons to be predicted. Weinberg and Salam also included an interaction with the scalar field to give the electron mass (like the gauge bosons, it also starts off massless before the symmetry is broken). Simply adding masses to the theory in a more arbitrary fashion would spoil too many of its properties. By having the masses arise by spontaneous symmetry breaking, some important features of the underlying gauge symmetry are preserved.

	Left to right: Sheldon Glashow, Abdus Salam and Steven Weinberg at the Nobel Ceremony for Physics, 1979 (photo copyright Scanpix Sweden)

Most important, it turns out that a spontaneously broken gauge theory can retain an essential property known as renormalisability. Neither Weinberg nor Salam proved that their model was renormalisable, but both conjectured that it could turn out to be the case. Proof of renormalisability came in 1971, from work by Gerard ’t Hooft. With that, the electroweak theory of the “Model of Leptons” was on a firm footing.

The Weinberg-Salam model used the simplest possible arrangement of scalar particles that could provide suitable symmetry breaking. As well as providing masses to the gauge bosons and the electron, the Higgs mechanism results in a massive scalar particle. This appears to be the Higgs particle as discovered at the LHC.

What’s Next?

The full Standard Model builds beyond Weinberg and Salam’s electroweak model by including quarks and gluons, and by including three generations of quarks and leptons. The weak interactions of all the quarks and leptons are governed by essentially the same theory as Weinberg’s model, with some added twists from the way that the generations are connected. The gluons are also governed by a Yang-Mills gauge theory (quantum chromodynamics, or QCD), but without any symmetry breaking. A different kind of vacuum effect called confinement locks the massless gluons inside particles such as protons and neutrons.

Although QCD and electroweak theory coexist comfortably in the Standard Model, in many respects they are not unified in the manner that Weinberg’s model of leptons unified electromagnetism and the weak interaction. Bringing gravity properly into the mix is another outstanding problem, pursued for decades by legions of string theorists and others.

There is probably nothing that physicists—including Weinberg—would like more, than to see signs from the LHC of his model failing or being surpassed, to provide an essential clue to the next step, a clue to a new model that can light the way for the next 50 years.

---- Graham Collins

Related links

A talk Weinberg gave to ICTP today can be watched on ICTP's YouTube channel.

CERN Courier: interview to Weinberg. 

CERN Courier: article with further details of the history and the physics behind the 1967 paper.