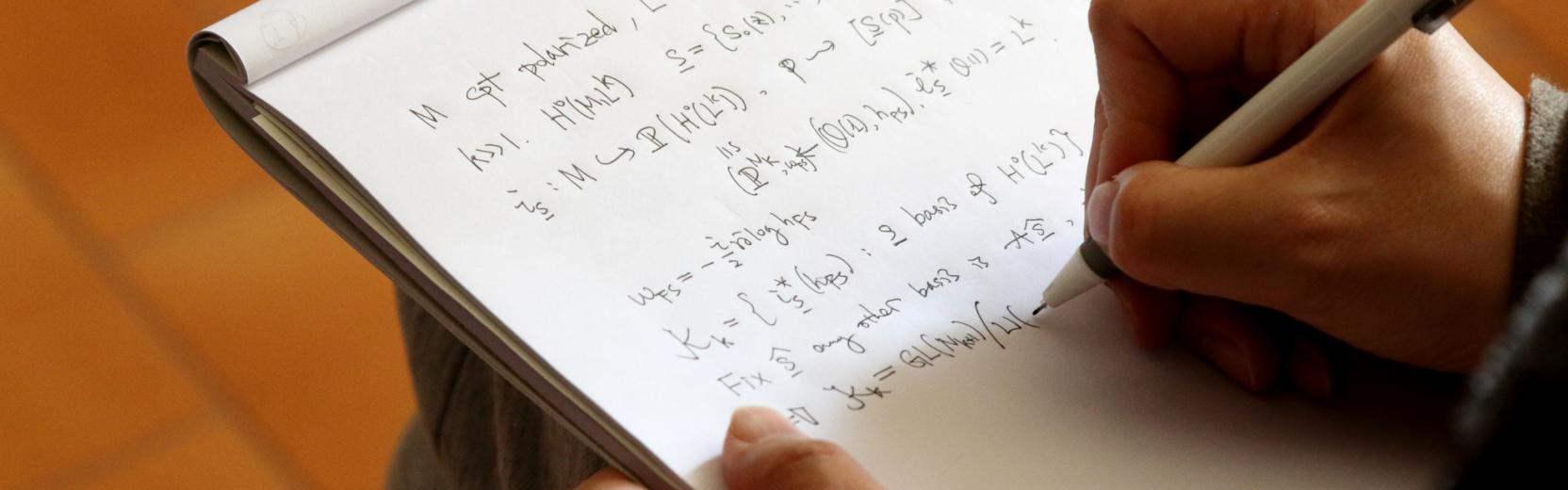There’s a casual air about mathematician Ian Agol that belies his intense, abstract mind. Dressed in shorts and sport sandals, he recently presented a colloquium at ICTP on the virtual fibering conjecture to a large audience including mathematicians who were attending ICTP’s Advanced School on Geometric Group Theory and Low-Dimensional Topology.
Agol has had a good year: he recently completed a 12-month sabbatical at the Institute for Advanced Study in Princeton, New Jersey, taking him away from his home base at the University of California, Berkeley, for an intense interlude with some of the brightest mathematicians in the world. Even more impressive, Agol was awarded the 2016 Breakthrough Prize in Mathematics for “spectacular contributions to low dimensional topology and geometric group theory”. Laureates receive a prize of US $3 million.
Agol studies the topology and geometry of three-dimensional spaces, such as our own universe. He credits his interest in this topic to the late mathematician William Thurston, whom he met at a summer program run by the Mathematical Sciences Research Institute in California. Agol recalls that at the time he was interested but “stuck” in knot theory—studying closed loops and strings. Thurston introduced him to a geometric approach to help tell when one knot can be deformed into another—a key goal in knot theory. “I found that appealing, and as I dug deeper into the subject I realized that there were some very powerful tools being developed by Thurston and others: mathematical tools, theorems and techniques, various sorts of mathematical constructs that tend to be broadly useful,” Agol explains.
These powerful techniques opened a new world for Agol, one that now included abstract ideas like higher dimensions. “That’s how things go in mathematics—it is a very abstract subject so you need a lot of motivation to learn this hard, abstract theory; having some concrete thing that motivates you is always beneficial,” he says.
Thurston’s influence challenged the way Agol thought about geometric problems, requiring him to form mental pictures of visualizations that take some time for the mind to develop. Those images then need to be translated into mathematics that are rigorous, and that can be written down and explained to other people. The process proved beneficial to Agol. “I developed a lot of intuition for three dimensional spaces, where you can visualize things much better, but certain aspects of that intuition carried over to thinking about higher dimensions and that was quite helpful,” he says.
It is difficult to imagine any type of mathematics being too challenging for this Breakthrough Prize winner. Yet Agol readily admits that his latest research interest—gauge theory, a mathematical concept often used by theoretical physicists to describe gauge bosons, the force carriers in subatomic physics—has been hard going. He hopes the theory will help him make connections between 3-manifold and 4-manifold topology. “I don’t know if it’s possible and I don’t really have any good ideas yet,” he laments, but then adds, philosophically, “Maybe I just won’t get anywhere and will have to do something else, but it is fun to learn new stuff.”
As for what to do with his multi-million-dollar Breakthrough Prize money, Agol plans to invest a large portion of it into mathematics education. He has already set aside US$100,000 for the Breakout Graduate Fellowships administered by the International Mathematical Union that support graduate students from developing countries. He also created a lectureship in honor of Thurston at the University of California-Davis, where Agol was a postdoctoral student.