The 2016 Nobel Prize in Physics was awarded "for theoretical discoveries of topological phase transitions and topological phases of matter." What does that mean?
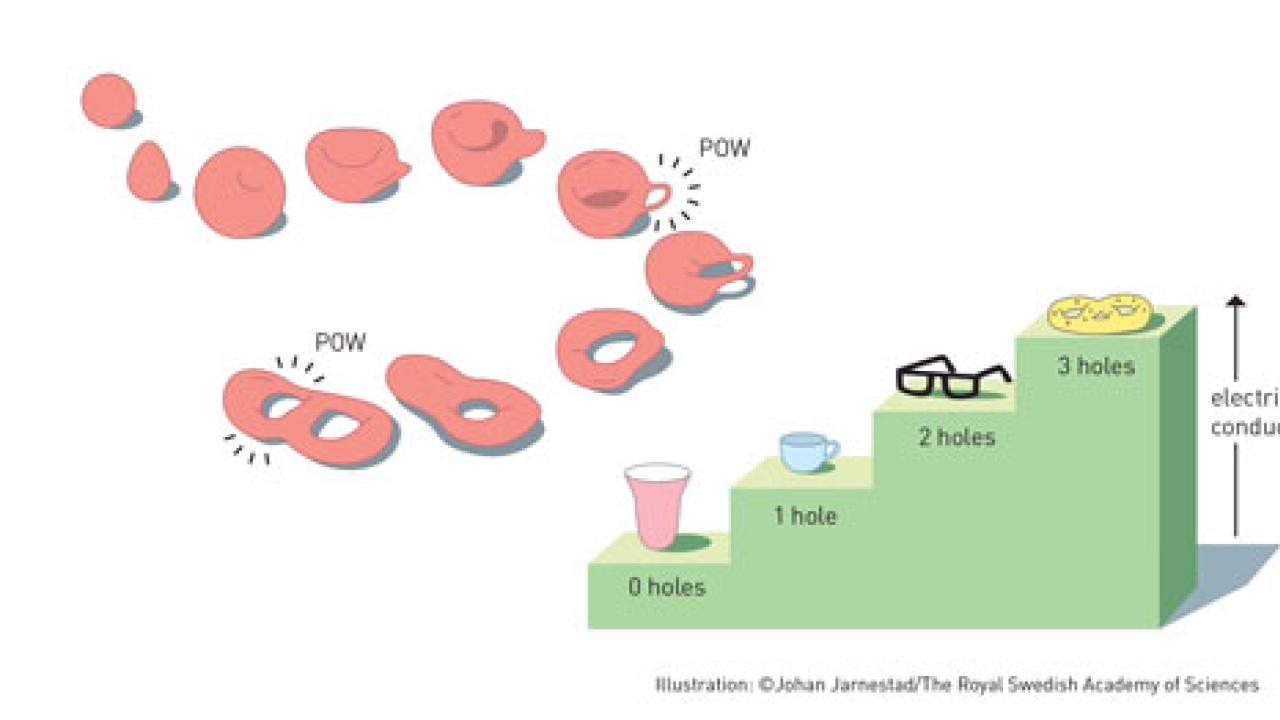
Topology, simply defined, is a field of study that describes step-like changes in a property. For example, to borrow an analogy presented during the announcement of the Nobel Prize in Physics, a pastry cannot have half a hole. It can have none and be a cinnamon bun, or it can have one and be a donut. If you bend that donut without breaking it, it is still a donut with one hole, even if it doesn't look the same. Certain properties of the donut have been maintained. These are known as topological properties, and their study has given rise to some fascinating physics.
Matter behaves classically at the scale and temperatures that we walk around in every day. But at much smaller scales, and when the temperature approaches absolute zero, quantum effects start to become important, producing sometimes bizarre behaviors of matter. These include the phase transitions investigated by David Thouless and Michael Kosterlitz--two of this year’s Nobel Laureates--which occur as a superconductor heats up from absolute zero, transitions that rest on both quantum mechanics and topological effects.
Superconductors rely on superfluidity, which happens when a lack of thermal energy causes all the particles in a substance to start behaving much more like interlocking waves—the wave characteristics of their wave-particle nature become dominant. Before Thouless and Kosterlitz, theoretical research said that superconductivity above complete absolute zero in fewer than three dimensions was not possible.
In 1972, Thouless and Kosterlitz found that instead, in a two dimensional system, superconductivity is possible but in a peculiar way. When the temperature isn't at exactly absolute zero, the added thermal energy causes defects in the wave-like field. These defects appear as spinning vortices, but instead of breaking the superfluidity and rendering the superconductor useless, the vortices pair up, their opposite rotations canceling each other out. The defect is still there, but the topological properties of the field is maintained, and superconductivity is possible.
Why care about two-dimensional systems? As it turns out, many superconductors are built in layers, which behave as though they are two-dimensional. Luckily, it turns out that thermal excitation does not break superconductivity until a critical temperature, when there is what's known as a Kosterlitz-Thouless phase transition.
Thouless later used topology to explain other bizarre behavior, what's now known as the integer Quantum Hall effect. If a semiconducting slab sits at right angles to a magnetic field, a voltage develops across the slab. But instead of increasing smoothly as the strength of the magnetic field increases smoothly, the voltage jumps up at specific intervals. In 1983, Thouless was able to link this phenomena mathematically to topological properties, explaining the jumps.
Inspired by this work, Duncan Haldane, this year’s third Physics Nobel Laureate and a close friend of ICTP, investigated what he calls a toy model, comprised of two chains of particles, each with different spin directions. He found that while a chain spinning in one way only needed a tiny amount of energy to disturb it, the chain spinning the opposite direction could resist large amounts of energy before getting ruffled. This led to work on topological insulators, materials that conduct electricity on their edges, but are insulators in their interiors, and opened the door to the creation of new types of materials based on controlling this topology.
Not only are new materials on the horizon thanks to this novel work, but interest in the field of topological physics is exploding. The great contributions of all three of the Nobel Laureates exposed a richness of questions and possibilities, inspiring many other physicists to investigate.
--Kelsey Calhoun