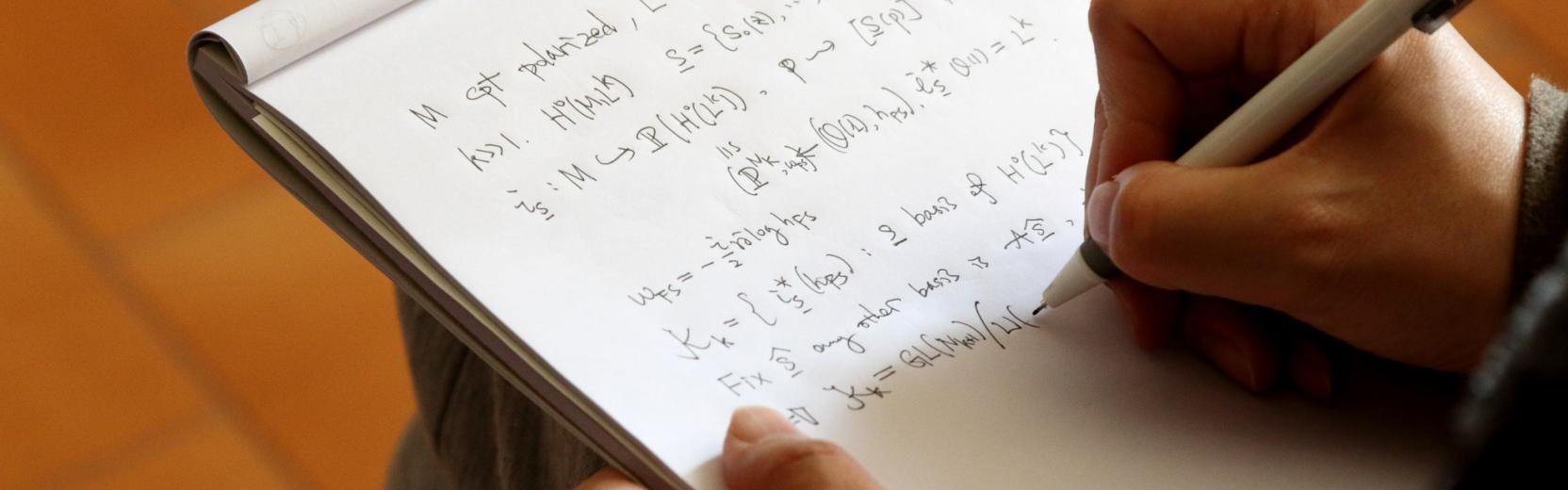Back
Research Areas
Next

Quantitative ecology and evolution
The questions that motivate our research concern fundamental aspects of the organization of highly diverse ecological communities. Why do so many species coexist in the same environment? What are the ecological forces shaping species occurrence, abundance, and variation across scales of space, time, and ecological organization? What is the functional role of diversity? How do ecological processes affect evolution within a population and how does evolution affect the ecological organization in complex, diverse communities? We approach these questions with a broad set of strategies and methods, which can be summarized in the tension between data-inspired modeling and model-driven data analysis. We develop theory in community ecology and population genetics, using the tools of stochastic processes, random matrix theory, statistical mechanics, and non-linear dynamics. We work with large sequencing datasets of environmental and experimental microbial communities, which we study by combining data-science techniques and mechanistic modeling. By combining theory, environmental and experimental data we aim at unveiling the ecological processes shaping the structure of complex (microbial) communities.

High-dimensional statistics, inference and theory of machine learning
The performance of modern inference and learning algorithms exploiting massive datasets for data science applications is improving at an incredible pace. Yet, the development of a theoretical framework to model these complex information processing systems and better quantify their potential and limits is still at its premises. QLS researchers investigate fundamental questions such as "What is the minimal amount of data needed to perform accurate predictions? When is it possible to infer and learn in a computationally efficient manner? What is the influence of data structure on the performance of inference algorithms?" The answers happen to be deeply linked to phase transition phenomena as arising in more classical physical systems. But this is more than an analogy. Therefore, to tackle these timely problems in a quantitative, mathematically rigorous manner, we often take an approach rooted in statistical physics combined with information theory, high-dimensional statistics, random matrix theory and the mathematical physics of spin glasses.
Stochastic thermodynamics
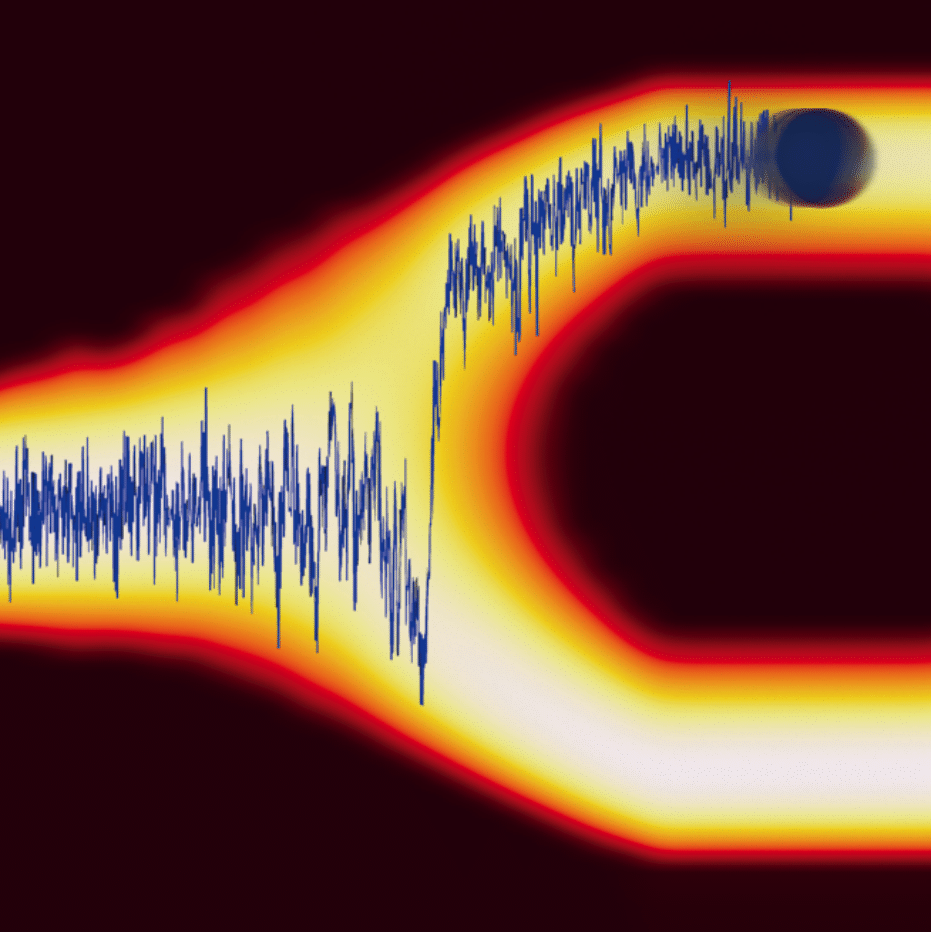
We investigate nonequilibrium fluctuations of microscopic systems using
stochastic thermodynamics. To this aim, we develop a holistic approach
combining theory, numerical simulation and experimental data analysis
that focuses on both fundamental questions and development of
applications. We pioneered the development of the martingale theory of
stochastic thermodynamics, and investigate its relevance to biological,
soft-matter, condensed matter and active systems. Another key goal of
our work is quantifying time irreversibility and entropy production of living systems as signatures of life and/or activity, as in e.g. the
spontaneous fluctuations of hair-cell bundles in the ear of the
bullfrog. Last but not least, we are also interested in finding
universal principles for the efficiency of energy harvesting from active
matter, and in applying concepts of stochastic thermodynamics in
perceptual decision making.

Emergent collective behaviour in interacting agent systems
Statistical mechanics provides quantitative methods to understand how collective behaviour may emerge from the interaction of simple units, not only in physics but also in economics and finance. This research can shed light on several phenomena, ranging from the loss of transparency in financial transformations (e.g. securitization) and the relation between inequality and growth, to the unintended consequences of technological innovation. This approach requires the use of advanced techniques of statistical mechanics of disordered systems in order to account for the heterogeneity of agents and of their interactions, and it allows us to scale-up insights from game theory to the collective level, showing, for example, the role that trust plays on ensuring systemic stability in social as well as in financial networks. A promising line of research builds on extending recent results of stochastic thermodynamics to finance. For example, no-free lunch (i.e. no-arbitrage) principles in finance (i.e. no gain can be extracted from trading) bear an intriguing similarity with the second law of thermodynamics (i.e. no work can be extracted from cyclic isothermal thermodynamic transformations). Can this similarity be put on more firm grounds?

Featureless statistical inference and learning
With the availability of high dimensional dataset on systems such as the brain, cells or an economy, statistical learning has entered a new era. The lack of knowledge on the system's "laws of motion" or on its function, and the high dimensionality of the data, call for a statistical approach that make no a priori assumptions. This is what we call featureless inference. Classical statistical learning stems from defining what is to be learned, and how and/or why it is to be learned, which then turns learning into an optimisation problem. A theory of learning in situations when even what is to be learned is unknown a priori needs to be based on a quantitative notion of relevance, because learning is about “making sense” of data that “make sense”, i.e. which is relevant. The notion of relevance, which we recently introduced, makes it possible to distinguish what is relevant from what is not in an absolute manner, even in the under-sampling domain, where data is high-dimensional and scarce. Understanding learning in this regime is crucial, since this is the regime where both living systems and artificial intelligence operate. Our approach to featureless inference is rooted in information theory and leads to a generic relation between maximally relevant datasets or representations and (statistical) criticality. It also predicts how learning machines should morph their energy landscapes in order to learn structured datasets. We have explored this approach both for new approaches to statistical inference (e.g. to identify relevant neurons in the brain or amino-acids in proteins) and for Bayesian model selection, and for a principled design of learning machines. Besides extending these results, the relation between maximal relevance and thermodynamic efficiency, using results of stochastic thermodynamics, is a promising further avenue of research that may provide further insights on why learning has evolved in living systems.
Efficiency of neural computation
Neural systems are intricate networks that perform functions. Our aim is to understand how computation emerges from their complex dynamics. We do this employing two parallel approaches. Using tools from statistical physics and theoretical machine learning, we study the impact of constraints on computation, deriving fundamental bounds for the function of biologically plausible neural networks. We are particularly focused on understanding quantitatively the role of heterogeneity in the dynamics and control of neural systems. In parallel, we build data-driven models for neural population dynamics, using large-scale recordings in behaving animals performing tasks. Our recent focus is on the efficiency of neural computation from both an information theoretic and energetic perspective.

Physics of behaviour and sensing
Individuals must make effective decisions in order to increase the amount of reward they can get from the environment. Choosing how and when to move is one specific behaviour that is often central to survival and proliferation of cells and organisms. This decision is often guided by chemical and mechanical cues, as well as by social interaction when the process happens at a collective level. These issues are studied in several model systems, ranging from chemotaxis in bacteria and cancer cells, to olfactory search in insects and soaring in birds. Combining ideas from statistical physics, information theory, computer science and biology, we aim at an algorithmic understanding of animal search behaviour and decision-making guided by sensory information.